흙은 독립된 흙 입자들 사이의 점착력 또는 마찰력에 의하여 불완전하게 결합되어 있어 외력에 의하여 쉽게 흐트러지는 특성이 있지만, 이러한 성토체의 내부에 흙과의 결속력이 우수하고 인장강도가 큰 재료(보강재)를 삽입하면 전단강도가 개선된 새로운 토체를 형성할 수 있는데, 이를 보강토(reinforced soil 또는 reinforced earth)라고 한다.
목차
- 보강토
- 보강토체의 전단강도 증가이론
- 겉보기 점착력 발생 이론
- 내부마찰각 증가 이론
- 보강토체 전단강도 증가이론의 합성
- 마무리
보강토
흙은 아주 훌륭한 건설재료 이지만, 독립된 흙 입자들 사이의 점착력 또는 마찰력에 의하여 불완전하게 결합되어 있는, 근본적으로 부스러지기 쉬운 흙 입자의 결합체로서, 외력을 받으면 쉽게 분리되어 르트러진다.
이러한 성토체 내부에 흙과의 결속력이 우수하고 인장강도가 큰 재료(보강재)를 삽입하면, 성토체 내부에서 발생하는 토압을 감소시키고 변형을 억제할 수 있는데, 이렇게 형성된 성토체를 보강토(reinforced soil 또는 reinforced earth)라고 한다.
보강토체의 전단강도 증가이론
아래 그림 1.에서는 모래에 대한 삼축압축시험결과 파괴된 공시체를 보여주며, 보강되지 않은 공시체(a)는 일반적인 흙 시료애서 발생하는 평면파괴가 발생하는 반면, 보강된 공시체에서는 보강재 층 사이에서 배부름(bulging)이 발생하여 삽입된 보강재가 모래의 횡방향 팽창을 효과적으로 억제하고 있음을 알 수 있다.

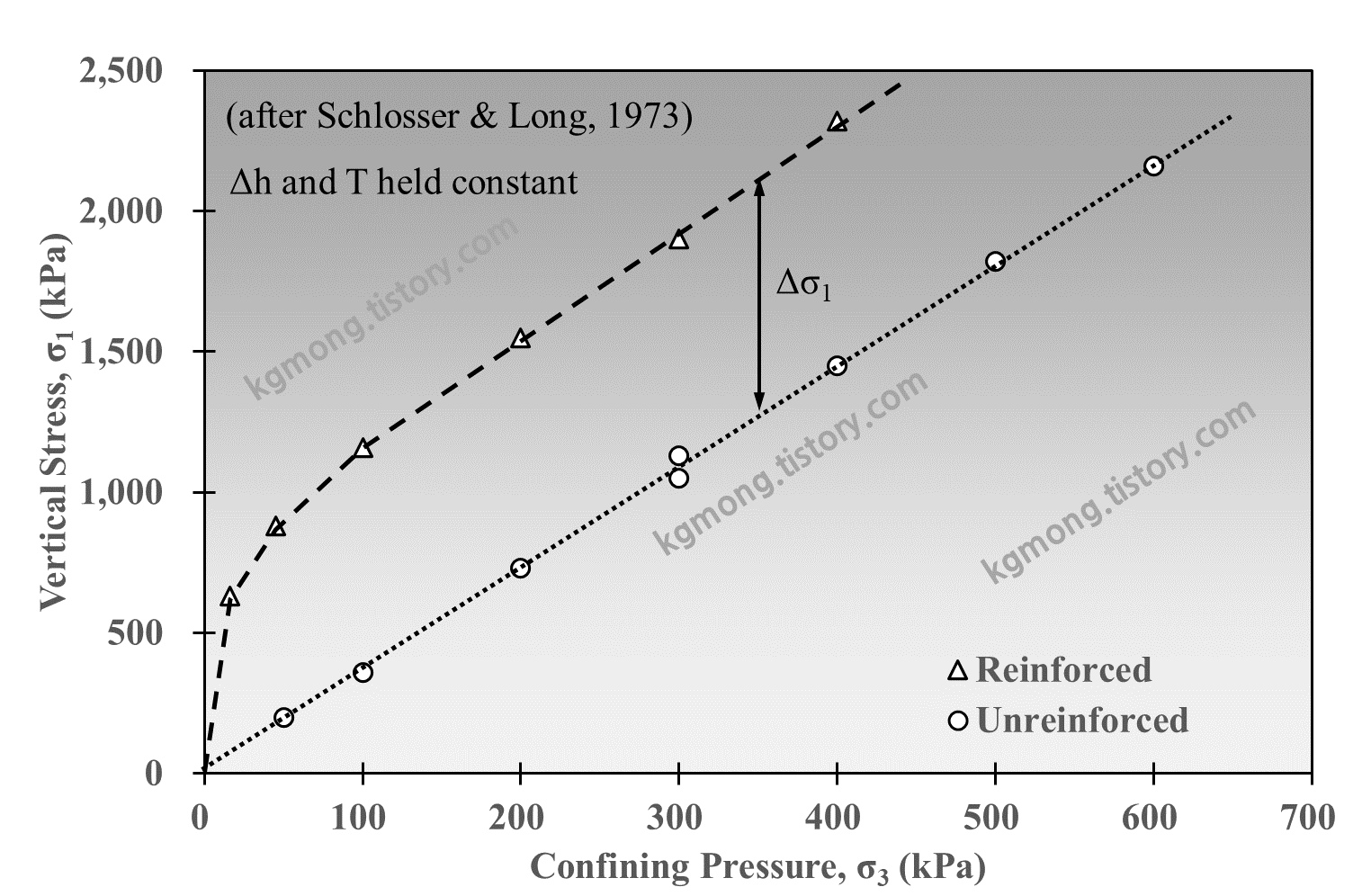
그림 3.에서는 보강된 모래 공시체에 대한 삼축압축시험 결과를 보여 주며, 보강된 공시체의 파괴 시 수직응력($\sigma_1 $)은 보강되지 않은 공시체의 수직응력 보다 커서 보강효과가 있다는 것을 알 수 있다. 보강재의 간격($\Delta h $)과 강도($T$)를 일정하게 유지한 경우, 구속압력($\sigma_3$)이 낮은 경우에는 구속압력($\sigma_3$)이 증가함에 따라 증가되는 수직응력($\Delta \sigma_1$)이 커지지만, 구속압력($\sigma_3$)이 어느 값 이상이 되면 구속압력($\sigma_3$)의 크기와 상관없이 증가되는 수직응력($\Delta \sigma_1$)은 일정하게 유지된다는 것을 알 수 있다.
겉보기 점착력 발생 이론
이 이론에서는 보강토체의 증가된 전단강도는 보강재에 의해 새롭게 발생한 점착력에 기인된다고 해석하는 이론으로, 다음 그림 4.에서와 같이 감소된 수평응력($\sigma_h$)을 가진 보강토체의 새로운 응력상태는 보강재에 의해 추가로 유발된 겉보기 점착력($c_r$)에 기인된다고 간주한다.

보강재에 의해 추가로 유발된 겉보기 점착력은 다음과 같이 계산할 수 있다.
보강된 흙 시료의 파괴포락선은 다음 식과 같이 정의되며, 여기서 2번째 항은 보강재에 의하여 유발된 응력이다.
$$K_a \sigma_v = \sigma_h + \sigma_r \tag {1}$$
위 식을 $\sigma_v$에 대하여 다시 정리하면,
$$\sigma_v = K_p \sigma_h + K_p \sigma_r \tag{2} $$
한편, 점착력과 내부마찰각이 있는 흙에 대한 Rankine-Bell의 방정식에 따르면 $\sigma_v$는 다음 식과 같이 나타낼 수 있다.
$$\sigma_v = K_p \sigma_h + 2 \sqrt{K_p} c_r \tag {3} $$
여기서, $c_r$은 보강으로 인하여 유발된 점착력
위 식 (2)와 식 (3)을 등식으로 정리하면
$$c_r = \frac{\sigma_r \sqrt{k_p}} {2} \tag{4} $$
내부마찰각 증가이론
내부마찰각 증가이론에서는 보강재의 삽입으로 인하여 복합토체에 내부마찰각이 증가($\phi$ $\rightarrow$ $\phi_r$)함으로서 보강토체의 전단강도가 증가한다고 설명한다.
즉, 토체 내부에 보강재가 삽입된 경우, 흙과 보강재 사이에는 마찰저항력이 발생하며, 이러한 마찰저항력에 의하여 보강재가 흡수힌 수평응력($\sigma_r$) 만큼토체 외부에서 저항해야할 수평응력이 감소하게 된다(그림 5.에서 $K_a \sigma_v $ $\rightarrow$ $\sigma_h$). 이러한 응력상태에 대하여 Mohr 응력원을 그리먄 그림 5.에서와 같이 비보강 시와는 전혀 다른 새로운 응력상태가 된다. 여기서, 흙과 보강재 사이의 마찰저항력은 보강재 위에 작용하는 응력에 비례하므로 보강 후의 파괴포락선은 그림 5.에서와 같이 수직응력에 비례하여 증가하는 형태가 되어 보강토체의 내부마찰각이 증가하는 결과과가 된다.

이러한 보강효과는 다음과 같이 식으로 표현할 수 있다.
$$\sigma_r = f \sigma_v \tag{5}$$
여기서, $\sigma_r$은 보강재에 의하여 감소된 수평응력 이고, $f$는 흙/보강재 사이의 마찰계수($= \tan \delta$) 이다.
이 때 내부마찰각 $\phi$로부터 증가된 마찰각 $\phi_r$은 마찰계수 $f$와 주동토압계수 $K_a$로부터 결정되며, 그림 5.로부터 다음과 같은 관계가 성립한다.
$$K_a \sigma_v = \sigma_h + \sigma_r \tag {6} $$
여기서, $K_a$는 주동토압계수 이고, $\sigma_h$는 수평토압 이다.
식 (5)를 식 (6)에 대입하여 정리하면
$$K_a = \frac{\sigma_h}{\sigma_v} + \frac{\sigma_r}{\sigma_v} = \frac{\sigma_h}{\sigma_v} + f \tag {7}$$
그림 5.에서 보강 후의 파괴포락선은 다음 식 (7)과 같은 관계가 성립하며, 보강토체에서의 보강효과는 주동토압계수의 감소($K_a$ $\rightarrow$ $K_{ar}$)로 나타난다.
$$ \frac{\sigma_h}{\sigma_v} = K_{ar} = \frac{1- \sin \phi_r}{1+ \sin \phi_r} \tag {8} $$
여기서, $K_ar$은 보강 후의 감소된 주동토압계수 이고, $\phi_r$은 보강 후의 증가된 내부마찰각 이다.
식 (7)과 식 (8)로부터 보강토체의 증가된 내부마찰각은 다음 식 (9)와 같이 표현할 수 있다.
$$ \sin \phi_r = \frac{1 + f - K_a}{1- f +K_a} \tag{9} $$
보강토체 전단강도 증가이론의 합성
여러 연구자들이 수행한 연구결과들을 종합하여 분석한 결과, 응력수준이 낮은 경우에는 흙과 보강재 사이의 미끄러짐 파괴가 우세하며, 응력수준이 높은 경우에는 보강재 자체의 파단에 의한 파괴가 우세하다는 것이 밝혀졌고, Hausmann(1976)은 이러한 결과들을 종합하여 보강토체의 전단강도 증가이론은 다음 그림 6.에서와 같이 합성하였다.

마무리
성토체 내부에 흙과의 결속력이 우수하고 인장강도가 큰 보강재를 삽입하면 전단강도가 개선된 보강토체를 형성할 수 있으며, 이러한 전단강도의 개선은 삽입된 보강재의 효과로 인하여 보강토체에는 새로운 겉보기 점착력이 발생하거나 또는 내부마찰각이 증가함으로서 얻어진다.
여러 연구자들의 연구결과를 종합해보면 응력수준이 낮은 경우에는 흙과 보강재 사이의 결속력의 부족으로 인한 파괴가 우세하여 응력수준에 비례하여 보강토체의 전단강도가 증가하므로 내부마찰각이 증가하게 되고, 응력수준은 높은 경우에는 흙과 보강재 사이의 결속력은 충분하나 보강재의 인장강도가 부족하여 보강재 파단에 의한 파괴가 우세하여 응력 수준과 상관없이 보강재의 인장강도에 대한 겉보기 점착력이 발생하여 보강토체의 전단강도가 증가하게 된다.
'보강토' 카테고리의 다른 글
| 흙-보강재 상호작용 (0) | 2023.07.07 |
|---|---|
| 보강토옹벽에서 다짐의 중요성 (0) | 2023.07.01 |
| 보강토 공법의 응용 (0) | 2023.06.29 |
| 건설재료로서 흙 (0) | 2023.06.27 |
| 보강토 공법 (0) | 2023.06.26 |
